ОГЭ Задание 3
Значение логического выражения
Штана Альберт Игоревич
Типы заданий № 3
В этой статье будет разобрано задание 3.
Рассмотрим типовые задачи из третьего задания ОГЭ по информатике.
Данное задание относится к базовому уровню сложности.
Время выполнения задания ≈ 3 минуты.
Третье задание из ОГЭ по информатике проверяет умение работать с логическим выражением. В логическом выражении могут использоваться союз И и союз ИЛИ. Пусть 0 - это ложь, 1 - Истина. Тогда напишем таблицу истинности для союза И и для союза ИЛИ.
Таблица истинности для союза И
| Выражение | Результат |
|---|---|
| 0 И 0 | 0 |
| 0 И 1 | 0 |
| 1 И 0 | 0 |
| 1 И 1 | 1 |
Союз И похож на умножение в математике. Если в логическом выражении присутствует 0 (ложь), то в итоге тоже получается 0 (ложь). Лишь две единицы дают тоже единицу.
Таблица истинности для союза ИЛИ
| Выражение | Результат |
|---|---|
| 0 ИЛИ 0 | 0 |
| 0 ИЛИ 1 | 1 |
| 1 ИЛИ 0 | 1 |
| 1 ИЛИ 1 | 1 |
Эта операция похоже на суммирование в математике. Лишь 1 или 1 даёт не 2, как в математике, а 1.
Задача 1 (Классическая)
Напишите наименьшее число X, для которого истинно высказывание:
(X > 16) И НЕ (X нечётное)
Решение:
Нужно, чтобы высказывание было истинным. Посмотрим, когда единица (истина) получается для союза И. Такое происходит только когда слева и справа стоят 1 (единицы).
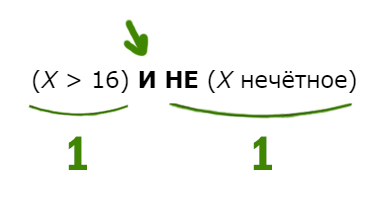
Получается наш X должен быть больше 16, и число должно быть не нечётное, т.е. чётное! Наименьшее чётное число большее 16 будет 18.
Ответ: 18
Задача 2 (Закрепление)
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 6) И НЕ (X >= 11)
Решение:
Опять высказывание должно быть истинным.
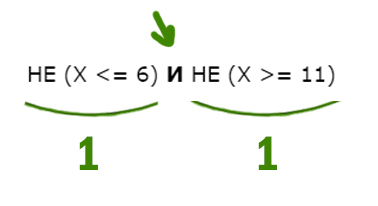
С одной стороны X должен быть НЕ меньше или равно 6, т.е значит, X нужно взять больше 6 (X > 6). Причём само число 6 не входит в этот диапазон.
С другой стороны X НЕ больше или равно 11, т.е. X должен быть меньше 11 (X < 11).
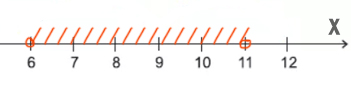
Наибольшее целое число будет 10.
Ответ: 10
Задача 3 (Союз И)
Напишите наименьшее натуральное двузначное число, для которого истинно высказывание:
НЕ (первая цифра нечётная) И (число делится на 3)
Решение:
Высказывание должно быть истинным.
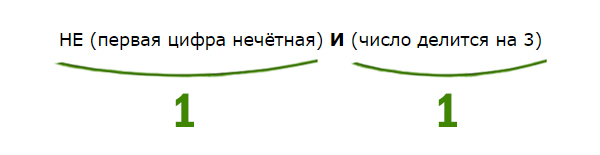
Первая цифра должна быть НЕ нечётная. Значит, она должна быть чётная. Число должно делится на 3. Найдём наименьшее двухзначное число, у которого первая цифра чётная, и оно делится на 3. Это будет 21.
Ответ: 21
Задача 4 (Союз ИЛИ)
Для какого целого числа X ЛОЖНО высказывание:
(X > 3) ИЛИ НЕ (X > 2)
Решение:
В этой задаче используется союз ИЛИ. Нужно, чтобы высказывание было ложным. Ложь при союзе ИЛИ получается только в одном случае, когда слева и справа стоят нули.
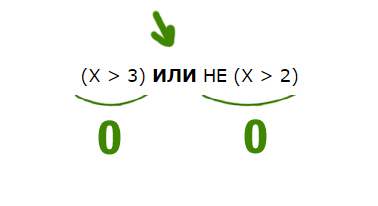
Утверждение, что X > 3 должно быть ложно, значит, если его перевернуть, получится X <= 3. Второе утверждение НЕ (X > 2) тоже должно быть ложно. Значит, если перевернём это утверждение, частицу НЕ нужно убрать. Получается просто X > 2.
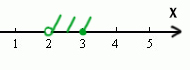
Получается, что только одно целое число входит в допустимый диапазон. Это тройка.
Ответ: 3
Задача 5 (Частица НЕ над всем выражением)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x<=200) ИЛИ (x<=100))
Решение:
Нам нужно сделать выражение истинным. Но всё выражение находится под влиянием частицы НЕ. Можно эту частицу полностью убрать, но воспринимать, как будто нужно сделать выражение ложным. А дальше всё как обычно. Ложь у союза ИЛИ получается в одном случае.
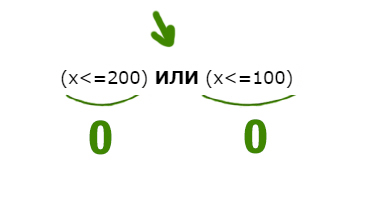
Первое выражение выдаёт ноль, когда x>200 (равно 200 не входит). Второе выражение выдаёт ноль, когда x>100. Объединив эти два условия получаем: x > 200.
Наименьшее число получается 201.
Ответ: 201
Задача 6 (Союз ИЛИ, закрепление)
Напишите наибольшее натуральное число x, для которого истинно высказывание:
(x < 5) ИЛИ НЕ (x > 3)
Решение:
ИЛИ выдаёт истину в трёх случаях. Либо первое выражение должно быть истинным, либо второе выражение должно быть истинным, либо оба выражения одновременно должны быть истинными.
Первое выражение истинно, когда x < 5. Второе выражение, когда x <= 3. Оба выражения истинны, когда x <=3.
Нам нужно наибольшее значение x, поэтому мы можем "выехать" на первом выражении. Ведь достаточно, чтобы оно было истинным. Получается ответ 4.
Ответ: 4
Задача 7 (Крепкий орешек)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x <= 100) ИЛИ (x>=200)) И (x чётное)
Решение:
В этой примерной задаче из ОГЭ по информатике применим все приёмы, которые мы разбирали до этого. Когда союз И выдаёт единицу?
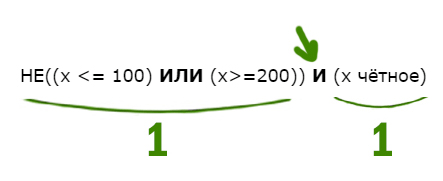
Посмотрим, когда левое выражение выдаёт 1. Уберём частицу НЕ, но тогда будем смотреть, когда левое выражение выдаёт 0.
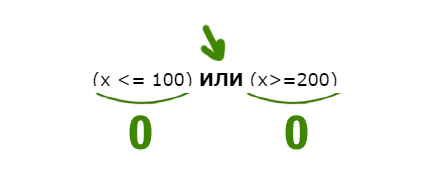
Перевернём оба выражения, которые находятся по обе стороны от союза ИЛИ. С одной стороны X>100, с другой X<200.
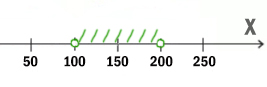
Учтём правое от союза И выражение. Наименьшее чётное число получается 102.
Ответ: 102
Задача 8 (ОГЭ 2026)
Напишите наименьшее натуральное число x, для которого ложно высказывание:
(x > 3) ИЛИ НЕ ((x < 4) И (x > 2)).
Решение:
В этой задаче из ОГЭ 2026 по информатике применим знания логических операций и приоритетов выполнения этих операций в выражении.
Последняя выполняемая логическая операция в выражении (x > 3) ИЛИ НЕ ((x < 4) И (x > 2)) – это операция ИЛИ. Когда ИЛИ нам выдаст 0 или ложь? Когда обе части(левая и правая): (x > 3) – ложь и НЕ ((x < 4) И (x > 2)) тоже ложь. Проверим сразу левую часть(поскольку она короче всего с неё и проще) когда она нам начнёт возвращать ложное значение? Сразу если x равен 3, то мы получим ложь в выражении (x > 3), т.к. (3 > 3) = 0(ложь). Проверим теперь правую часть от ИЛИ: НЕ ((x < 4) И (x > 2)). Сначала выполняем выражения во вложенных скобках, подставляем вместо x число 3. (x < 4) => (3 < 4) = 1(правда); (x > 2) => (3 > 2) = 1(тоже правда); (3 < 4) И (3 > 2) = 1(поскольку для И оба выражения дали 1, только тогда после И тоже будет 1). Осталось выполнить инверсию НЕ: НЕ ((3 < 4) И (3 > 2)) = 0(всё выражение с И в скобках, которое было 1 – меняется на ложь т.е. 0). Получилось что число 3 нам подходит в качестве ответа.
Чтобы убедиться с ответом, ещё раз проверим всё выражение с меньшим на единицу (чем 3) числом – с двойкой. Подставим вместо x теперь число 2. Проверим левую часть: (x > 3) => (2 > 3) = 0. С ней всё получается, а что же с правой частью выражения? Подставим 2 в правую часть выражения: НЕ ((x < 4) И (x > 2)) => НЕ ((2 < 4) И (2 > 2)). (2 < 4) = 1; (2 > 2) = 0; 1 И 0 = 0; НЕ 0 = 1. Получилось, что в правой части выражения мы получили при x = 2 – 1(или правду). Нам это уже не подходит потому что 0 ИЛИ 1 в конечном итоге даст нам 1, ане 0 как необходимо по условию задачи. Значит x мы не можем взять числом 2 и всё что менее 2, правая часть будет тогда возвращать нам 1. То же самое получится если мы возьмём число больше 3, например 4 и так далее, левая часть вернёт нам 1. Всё что остаётся это единственное число 3 когда всё выражение нам вернёт ложь и будет ответом.
Ответ: 3